繰り下がりのある筆算を指導した時のお話をしたいと思います。

４５－９は正解するけど

指導した生徒は、45-9や99-7といった計算は筆算を使わず解けます。指を使いながら解いていましたが、46-19といったように二桁と二桁を引くとなると、指を使うことが出来ないので、解けませんでした。

パターンを見つける

生徒は知的障がいもあり、一の位や十の位といった概念は理解できませんでした。しかし、計算する力はあったので、パターン化させると解けるようになるのではと考えました。

一見簡単そうに思えますが、パターンを見つけるまでは苦労します。どういうパターンが理解しやすいのか、一人一人違うため、生徒の反応を見ながら授業を進めていきました。

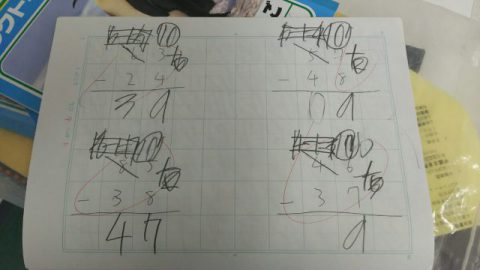
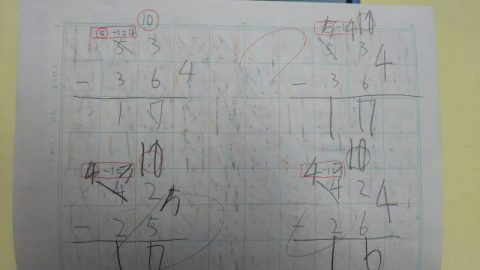
指を使って計算できるので、いかにしてその強みを活かせるか考えたところ、写真のように四角と丸の囲いを予め書き、計算させることにしました。

53の上の四角内には予め-1を書いておき、十の位が5なので5-1と計算することを示します。次に、丸の中には10を必ず書くように指示をしました。そして10-6を引かせ、4+3をして答えは7、4-3をして1と書き、答えは17であると教えました。

このように、最初の問題は私が手本として書いて示し、同じ問題を手本を見ながら同じように書いてもらいました。このやり方は効果があったのですが、若干の変更点が後々出てきました。

もっと分かりやすく

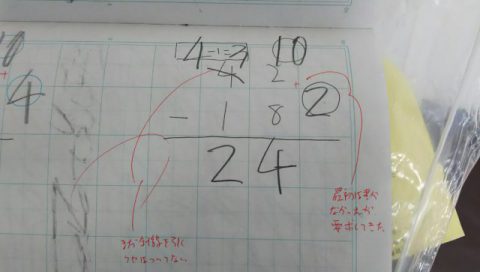
数をこなしていく内に、もっと丸の枠があった方が良いと判断して、写真のように10-8の答えを書く丸枠を書きました。さらに、生徒自ら＋のマークを書いて欲しいと手振り（言葉があまり出ないタイプのため）で要求してきたので、＋を加えました。

そこからです。サクサクと繰り下がりのある筆算の問題を自ら解けるようになってきたのは。

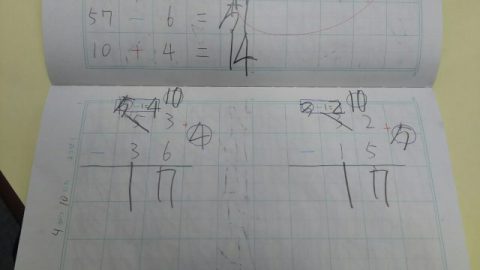
とても調子良く解けるようになったのですが、ここで問題が発生しました。

写真にあるように、十の位が0になる時は何が何でも0を書かないと気が済まない、こだわってしまったんです。このこだわりから脱却するのに時間がかかりました。下手に否定するとパニックになってしまうので、反応を見ながら傷つきにくい方法を探しました。

最終的にフセンを貼ったら書かないということを発見し、十の位が0になる問題は予め十の位にふせんを貼るようにしました。そうしていく内にこだわりが薄まっていき、いつしかフセンを貼らなくても平気になるようになりました。

繰り下がりのある筆算の計算はできるようになったので、現在は筆算の勉強はしていないのですが、せっかくの機会なので、今でも覚えているか後日試してみようと思います。